当然可以，以下是加粗了名词的版本：

“# 实验 5 干涉仪

1 目的

在本实验中，您将使用一个干涉仪基础装置，该装置设计为可用于迈克耳孙或法布里-佩罗模式。在实验的第一部分，您将设置设备以分别测量氦氖激光的波长。确定激光波长后，您将测量空气的折射率。

警告：在处理所有真空室、镜子和透镜时，请从侧面拿取，以防止留下指纹。带有指纹的镜片和镜子可能会影响实验结果。

警告：在开启激光之前，请检查所有镜子和透镜，确保它们没有指纹。如果有指纹，请使用异丙醇和提供的干擦布擦拭掉。

2 引言

干涉仪是一种将光束分成几部分，然后再将它们重新组合以形成干涉图样的设备。这个图样可以用来以极高的精度测量光的波长（或其他长度）。在干涉中，我们自然指的是波在重叠时的行为。当两波相遇时，结果波是两波的和。干涉可以是完全建构性干涉、完全破坏性干涉，或者是两者的组合（见图 5.1）。干涉的程度取决于组成波的相对相位。

3 法布里-佩罗干涉仪

在法布里-佩罗干涉仪中，两个部分镜子平行对准，形成一个反射腔。图 5.2 显示了一束光进入这样的腔体并在其中来回反射。在每次反射时，部分光束会透过，分裂每条入射光为一系列光束。由于透过的光束都来自同一入射光束，它们具有恒定的相位关系（假设使用的是足够相干的光源）。

透过光束之间的相位关系取决于每束光进入腔体的角度和两个镜子之间的距离。结果是一个圆形的干涉条纹图案，这些条纹既细又亮，并且间距较大。图 5.3 显示了这种图案的一个例子。法布里-佩罗条纹的清晰度使其在高分辨率光谱学中成为一个有价值的工具。通过移动其中一面镜子，可以改变光束之间的距离（从而改变相位关系），并使条纹图样发生偏移。当可动镜子平移一个距离 $\lambda / 2$ 时，新的条纹图案与原始条纹图案相同：

$$\lambda=\frac{2 d_{m}}{m}$$

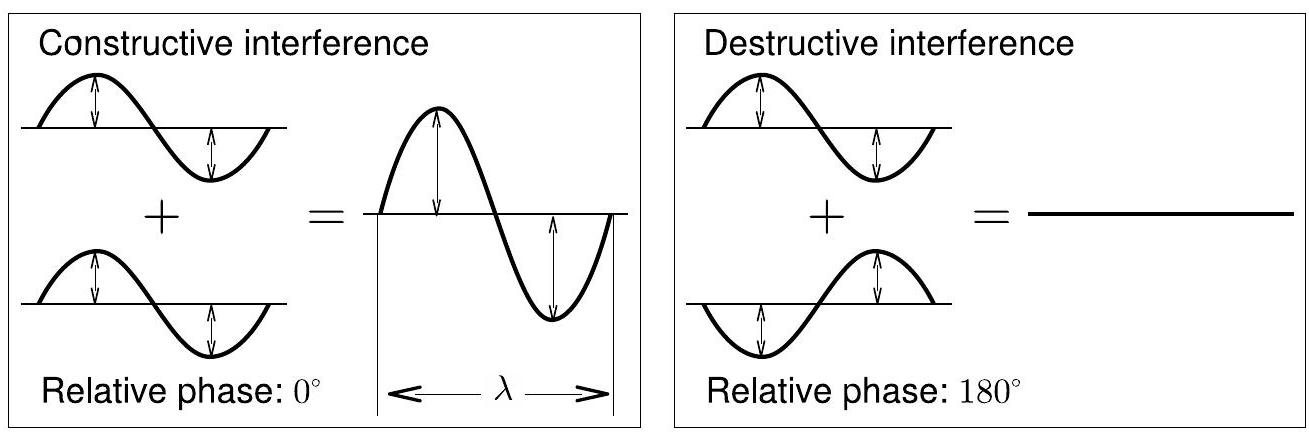
图 5.1：两波的完全建构性和完全破坏性干涉。

4 迈克耳孙干涉仪

A.A. 迈克耳孙于1881年设计并建造了干涉仪，用来检验“以太”的存在，这是一个假设的介质，人们认为光是通过它传播的，就像水中的波一样${ }^{1}$。如今，迈克耳孙干涉仪用于多种任务，包括测量光的波长、测量极小的距离以及研究光学介质。最著名的版本是一个长达3英里的版本，叫做激光干涉引力波天文台（LIGO），用于探测引力波（其联合创始人获得了2016年诺贝尔物理学奖！）。

图 5.4 显示了迈克耳孙干涉仪的示意图。一束来自激光的光线撞击一个光束分离器，分离器反射50％的入射光并透射另外50％。因此，入射光束被分成两束：一束传向可动镜子$\left(M_{1}\right)$，另一束反射向固定位置、可调角度的镜子$\left(M_{2}\right)$。两面镜子将光线直接反射回光束分离器。$M_{1}$反射的部分光线从光束分离器反射到观察屏，而$M_{2}$反射的部分光线透过光束分离器到达观察屏，在那里与$M_{1}$的光线发生干涉。

由于两束干涉光线来自相同的初始光束，它们最初是同相的。因此，当它们在观察屏上的某一点相遇时，它们的相对相位仅取决于它们的光学路径长度差 $\Delta l$。

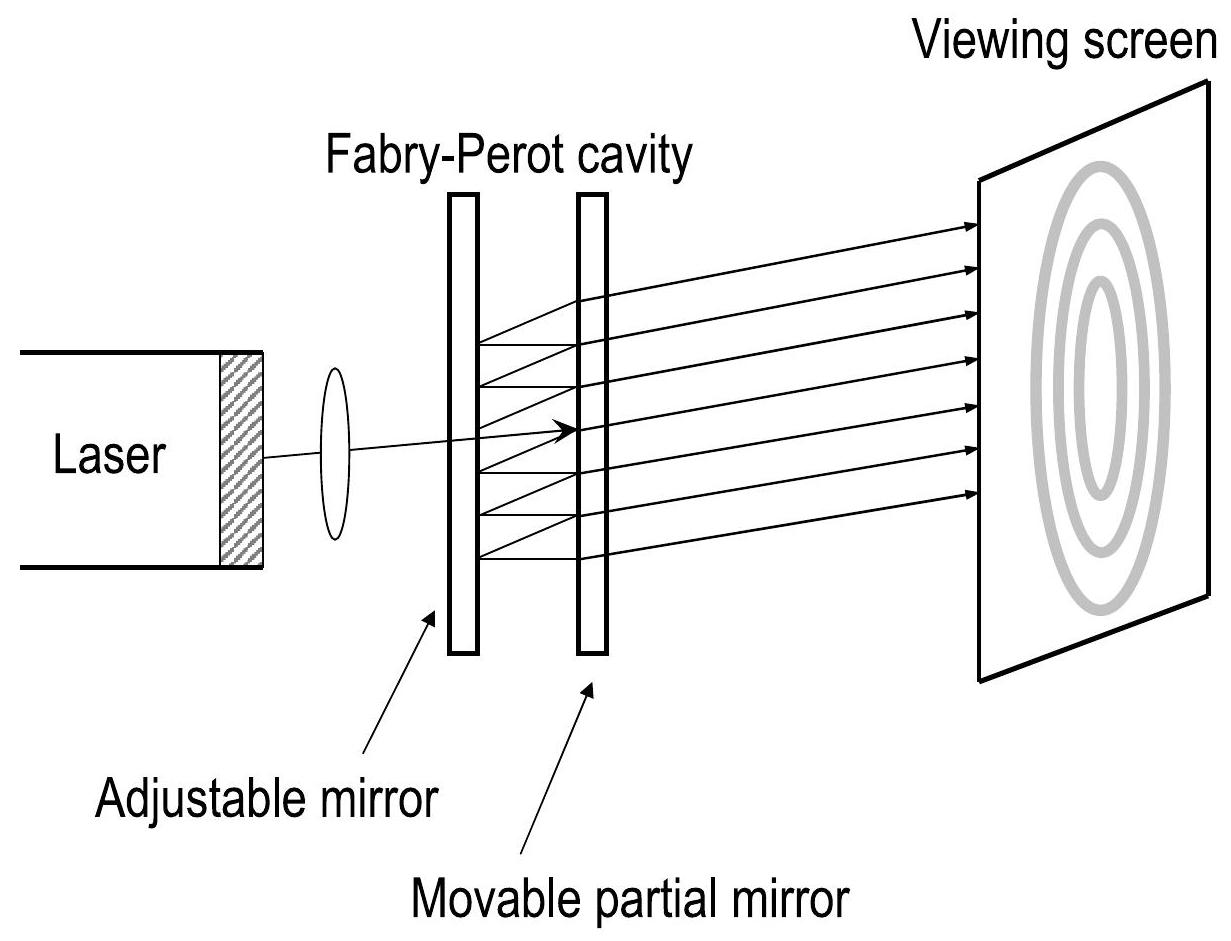
图 5.2：法布里-佩罗干涉仪示意图。该设备使用腔体将每束光分成一系列光束。（为清晰起见，腔内的反射有所偏移。）

证明以下几点：

1. 通过移动$M_{1}$，可以改变其中一束光的路径长度。
2. 将$M_{1}$移动$\lambda / 4$（四分之一波长）靠近光束分离器，将减少该光束的总光学路径长度$\lambda / 2$。
3. 移动$M_{1}$将导致屏幕上的干涉图样发生变化。

通过缓慢移动镜子一定的距离$d_{m}$并计数$m$，即干涉图样恢复到原始状态的次数，可以计算光的波长$\lambda$为：

$$\lambda=\frac{2 d_{m}}{m} \tag{5.1}$$

反之，如果波长$\lambda$已经知道，可以反向操作并估算位置变化$d_{m}$。通过这种方式，干涉仪可以用来测量极小的距离尺度。

图 5.3：干涉仪生成的类似条纹的干涉图案示例。

5 空气的折射率

5.1 引言

在迈克耳孙干涉仪中，条纹图案的特性取决于两束干涉光之间的相位关系。改变这种相位关系有两种方法：第一种是改变一束或两束光的传播距离（例如，通过移动可动镜子）；第二种是改变光束通过的介质。第二种方法可以用来测量空气的折射率。

当光穿过某些介质时，其波长$\lambda$根据以下公式变化：

$$\lambda=\frac{\lambda_{0}}{n}$$

其中，$\lambda_{0}$是光在真空中的波长，$n$是介质的折射率。对于较低的压力，气体的折射率与气体压力线性变化。随着折射率的变化，介质中的波长$\lambda$也会发生变化。

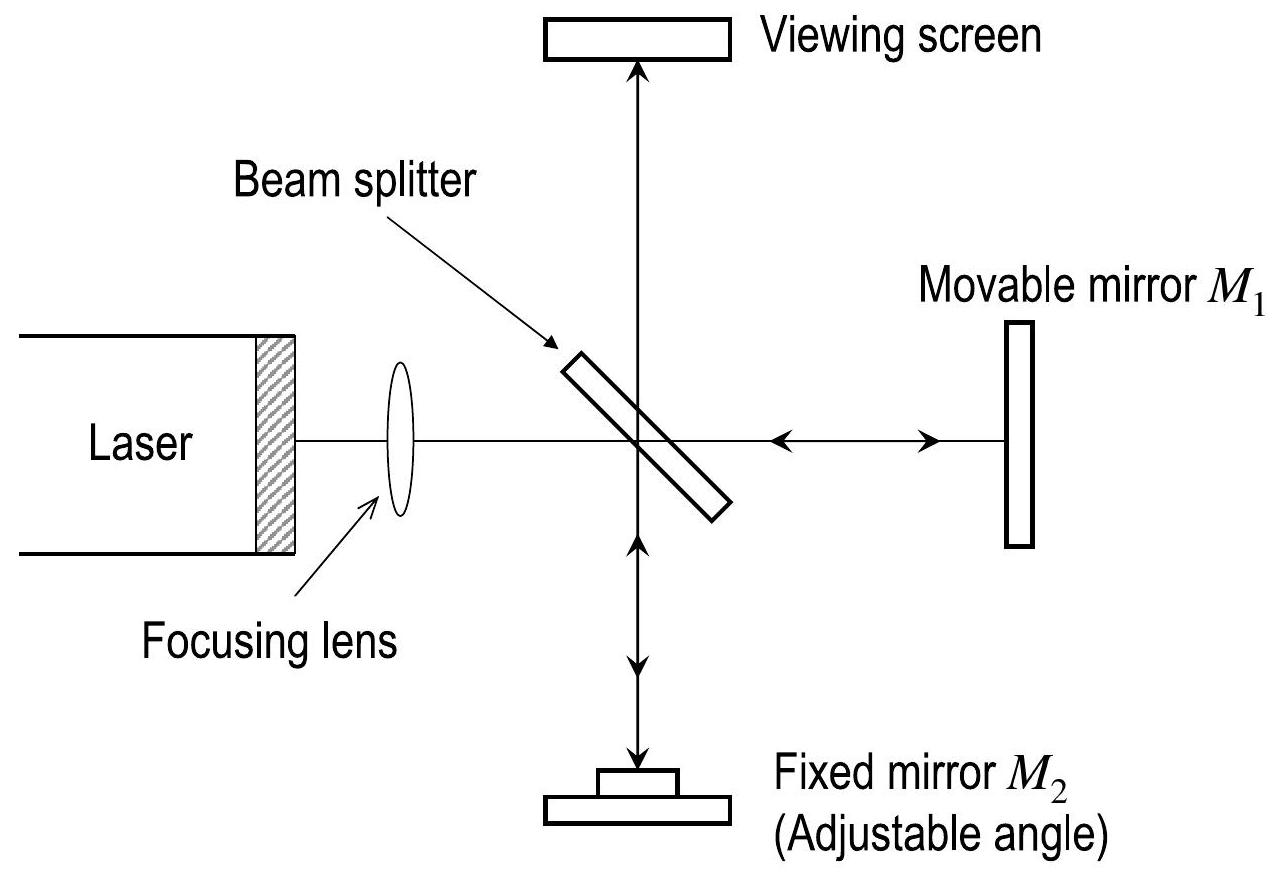
图 5.4：迈克耳孙干涉仪示意图。单束光通过半银镜分成两束。两束光之间的路径差由可动镜子变化。

5.2 压力与空气折射率变化

您将通过将真空室放置在迈克耳孙干涉仪的一个光路上来求取 $n_{\text {air }}$。当您将空气从真空室中抽出时，室内光的波长相对于室外波长将增加。这会导致干涉图案发生偏移。

最初，真空室内有 $N_{i}=2 d / \lambda_{i}$ 个光的波长（考虑到激光束经过真空室两次，分别是前进和返回）。在最终压力下，室内有 $N_{f}=2 d / \lambda_{f}$ 个波长。它们之间的差值等于您可能观察到的条纹数量。因此，$m=N_{f}-N_{i}=2 d\left(n_{f}-n_{i}\right) / \lambda_{0}$，或者

$$\begin{equation*} n_{f}-n_{i}=\frac{m \lambda_{0}}{2 d} \tag{5.2} \end{equation*}$$

真空室

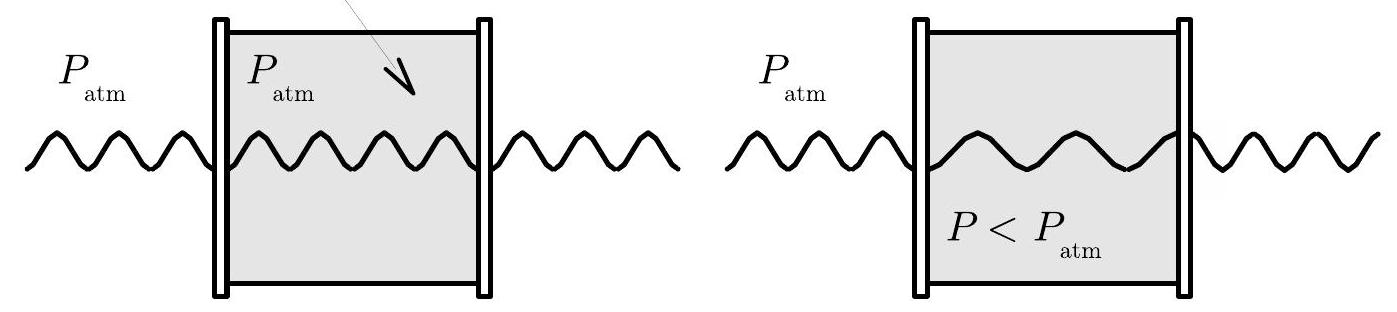
图 5.5：当空气被抽出时，真空室中光波长的变化。

6 实验

6.1 激光设置

在开始之前

警告：处理所有真空室、镜子和透镜时，请从侧面拿取，以防止留下指纹。带有指纹的镜片和镜子可能会影响实验结果。

警告：在开启激光之前，请检查所有镜子和透镜，确保它们没有指纹。如果有指纹，请使用异丙醇和提供的干擦布擦拭掉。

---

将干涉仪基础装置放置在实验桌上，确保千分尺旋钮指向您。

将激光对准台放置在干涉仪基础的左侧，约与干涉仪基础垂直，并将激光放在对准台上。

将一个组件支架（52-54）固定在干涉仪基础的左侧，另一个固定在右侧，两个都朝向内侧。

打开激光。使用激光台上的调平螺丝调整其高度，直到激光束通过两个组件支架的中心。（使用纸张检查光束路径。）您可能还需要稍微移动激光台，以调整激光的水平路径。最方便的方法是轻轻地将激光台后端横向滑动。

将可动镜子（58）放置在干涉仪基础上的凹槽内。

检查光束是否从可动镜子附近反射回来并接近激光口，并固定镜子。（如果没有，您可能需要对可动镜子的位置和/或激光的对准进行小的调整，直到正确为止。）现在，您准备好在干涉仪的任何操作模式下进行设置。”

当然可以，以下是加粗了名词的版本：

“ 检查光束是否从可动镜子附近反射回来并接近激光口，并固定镜子。（如果没有，您可能需要对可动镜子的位置和/或激光的对准进行小的调整，直到正确为止。）现在，您准备好在干涉仪的任何操作模式下进行设置。

6.2 测量激光波长（法布里-佩罗模式）

法布里-佩罗干涉仪仅在实验开始时使用一次，用来测量激光光的波长。

1. 按照上述激光部分的描述对激光和干涉仪基础进行对准。
2. 将可调镜子（51）安装在干涉仪基础上，处于法布里-佩罗位置，面朝可动镜子。
3. 使用其磁性支架将观察屏（62）放置在可动镜子后面的组件支架上。您应该能在观察屏上看到几束激光束的图像。
4. 使用拇指螺钉调整可调镜子的倾斜角度，直到屏幕上只有一个明亮的点。
5. 将18毫米焦距透镜 $(63,64)$ 安装在激光前组件支架的磁性支架上，使透镜位于离激光最远的组件支架的一侧。调整透镜位置，直到发散光束与可调镜子对齐。观察屏上应能看到清晰的干涉图样。

现在，您准备好测量激光的波长。

1. 调整千分尺旋钮至中间读数（大约 $500 \mu \mathrm{~m}$）。此时，千分尺读数与镜子运动的关系最接近线性。
2. 将千分尺旋钮逆时针旋转一整圈。继续逆时针旋转，直到旋钮的零位与指示标对齐。记录千分尺的读数。
3. 调整观察屏的位置，使毫米刻度上的一个标记与干涉图案中的一个条纹对齐。您可能会发现，如果参考标记距图案中心一到两个条纹，计数会更容易，或者您可能会发现数“靶心”更容易。
4. 慢慢地逆时针旋转千分尺旋钮。当条纹通过参考标记时，数一下它们。继续数，直到有一个预定数量的条纹（至少20个）通过您的标记。当您完成计数时，条纹应该与您开始计数时的位置一致。记录千分尺表盘的最终读数。
5. 记录 $d_{m}$，即根据千分尺旋钮读数记录的可动镜子向光束分离器移动的距离。记住，千分尺上的每个小刻度对应于$1 \mu \mathrm{~m}\left(10^{-6} \mathrm{~m}\right)$的镜子运动。
6. 记录 $m$，即您计数的条纹过渡次数。
7. 对以上步骤进行5次重复试验，每次记录结果。

6.3 测量激光波长（迈克耳孙模式）

1. 移除18毫米焦距透镜 $(63,64)$。
2. 将可调镜子安装在干涉仪基础上，处于迈克耳孙位置。将第二个组件支架放置在可调镜子对面，并将观察屏安装在其磁性支架上。
3. 将光束分离器（55）放置在激光光束的$45^{\circ}$角度内，位于裁剪标记内，使得光束被反射到可调镜子。根据需要调整光束分离器的角度，直到反射光束接近可调镜子的中心。
4. 现在，观察屏上应有两组明亮的点；一组来自固定镜子，另一组来自可动镜子。每组点应包括一个明亮点和两个较暗的点（由于多次反射）。再次调整光束分离器的角度，直到两组点尽可能接近，然后紧固拇指螺钉以固定光束分离器。
5. 使用可调镜子背面的拇指螺钉，调整镜子的倾斜角度，直到观察屏上的两组点重合。
6. 将18毫米焦距透镜 $(63,64)$ 安装在激光前组件支架的磁性支架上，使透镜位于离激光最远的组件支架的一侧。调整透镜的位置，直到发散光束与光束分离器对齐。您应该能看到圆形的条纹。如果没有，请仔细调整可调镜子的倾斜角度，直到条纹出现。

您现在将重复在法布里-佩罗设置中进行的激光波长测量，您可以参考第55页的说明。

• 记录 $m$，即您计数的条纹过渡次数，并记录千分尺旋钮的最终位置，共进行5次试验。

6.4 测量空气的折射率

为了测量空气的折射率 $n_{i}$，我们将抽出真空室中的空气，并测量在某一压力变化 $P_{f}-P_{i}$ 下条纹数量 $m$ 的变化。一旦知道压力变化如何影响折射率，就可以通过已知 $P_{f}$、$P_{i}$ 和 $n_{f}$ 来确定空气的折射率 $n_{i}$。当我们抽出室内空气时，会发生以下两件事：

1. 室内的压力下降 $\Delta P=P_{f}-P_{i}$
2. 折射率 $n_{f}$ 减小。回想一下，绝对真空的折射率定义为 $n_{\text {vacuum }}=1$。

将方程 (5.2) 两边除以 $\Delta P$，得到：

$$\begin{equation*} \frac{n_{f}-n_{i}}{P_{f}-P_{i}}=\frac{m \lambda_{0}}{2 d} \frac{1}{P_{f}-P_{i}} \tag{5.3} \end{equation*}$$

左边的量是 $n$ 对 $P$ 图的斜率。由于我们假设折射率与压力（在低压力下）线性变化，因此对于任何 $n$ 和 $P$ 之间的差异，这一比值是常数。因此，我们可以将公式重新写为线性方程：

$$\begin{equation*} n_{f}-n_{i}=C\left(P_{f}-P_{i}\right) \tag{5.4} \end{equation*}$$

其中 $C$ 是一个将通过实验确定的常数。由于左侧是常数，因此方程右侧的量也是常数。

$$\begin{equation*} C=\frac{m \lambda_{0}}{2 d} \frac{1}{P_{f}-P_{i}} \tag{5.5} \end{equation*}$$

1. 使激光器和干涉仪在迈克耳孙模式下对准。
2. 将旋转指针放置在可动镜子和光束分离器之间。
3. 将真空室附加到其磁性支架上，并将真空泵的空气管插入室体的空气出口孔中。
4. 根据需要调整固定镜子的对准，使干涉图案的中心清晰可见。图案会因真空室玻璃端板的不规则性而稍微扭曲，但这不是主要问题。
5. 为了进行准确测量，真空室的端板必须与激光光束垂直。旋转真空室并观察条纹。根据您的观察，如何确认真空室是否正确对准？

现在，您准备好测量激光波长。

1. 在真空室处于大气压力下开始，收集随着室内压力变化而发生的条纹数数据。
2. 缓慢转动泵手柄，使空气从真空室中排出，并记录在该时间间隔内通过的条纹数 $m$ 和该时间段结束时的压力 $P$。
3. 注意，您测量的压力实际上是表压 $P-P_{\text {atm }}$，因为表计在室内处于大气压力时从零开始。将您的 $\Delta N$ 值转换为 $m=N-N_{\mathrm{atm}}$，即在给定压力下的条纹数减去对应大气压力下的条纹数。（您不知道 $N_{\text {atm }}$，即大气压力下的条纹数，但您可以确定从开始排气到现在已经经过的条纹数，这就是 $m=N-N_{\text {atm}}$）。获取至少7个不同的 $m$ 和 $\Delta P$ 数据点。
4. 使用公式 (5.2) 将您的 $m$ 转换为 $n-n_{\text {atm }}$。

注意：以下数据将派上用场：

$$\begin{aligned} P_{\mathrm{atm}} & =76 \mathrm{~cm} \mathrm{Hg} \\ P_{\text {vacuum }} & =0 \mathrm{~cm} \mathrm{Hg} \\ d & =3.0 \mathrm{~cm} \end{aligned}$$

6.5 数据总结：

法布里-佩罗部分：

= $m, d_{m}$ 五次实验

迈克耳孙部分：

= $m, d_{m}$ 五次实验

+$m, \Delta P$ 若干次实验”

当然可以，以下是加粗了名词的版本：

“

7 精确计数条纹的建议

1. 干涉图样不需要完全对称或锐利。只要您能够清楚地区分最大值和最小值，您就可以进行准确的测量。
2. 计数条纹时容易失误。集中精力关注离中心较远的条纹，或者使用“消失靶心”技术，观察中心的最小值来计数条纹，可能会有所帮助。
3. 当转动千分尺旋钮计数条纹时，始终在开始计数之前先旋转一整圈，然后继续在同一方向旋转并计数。这样几乎可以完全消除由千分尺运动反向时的反向间隙引起的误差。（反向间隙是机械系统反转运动方向时总会发生的轻微滑移。）顺时针旋转千分尺旋钮会将可动镜子向右移动。
4. 始终进行多次读数并求取平均值，或让多个人计数同一实验并比较结果。
5. 预热激光器，以减少强度和极化变化。

8 分析

8.1 激光波长

1. 对于激光波长的测量，使用条纹数 $m$ 和可动镜子移动的距离 $d_{m}$，将它们转换为波长。
2. 计算这些波长的平均值，并求取均值的标准差：$\bar{\lambda} \pm \sigma_{\bar{\lambda}}$。
3. 比较两种不同方法的结果。它们是否在误差范围内一致？哪种方法似乎更准确？

8.2 空气的折射率

1. 绘制 $n-n_{\text {atm }}$ 与 $P-P_{\text {atm }}$ 的图表。
2. 绘制最佳拟合线并确定斜率 $C$。这个斜率与方程 (5.3) 中描述的比率略有不同。然而，您应该能够证明，改变 $x$ 和 $y$ 的值通过常数 $n_{\text {atm }}$ 和 $P_{\text {atm }}$，不会改变斜率（这些常数值在计算斜率时会被抵消）。因此，我们可以使用我们的图表 $n-n_{\mathrm{atm}}$ 对 $P-P_{\text {atm}}$ 来确定常数 $C$。
3. 一旦您知道了拟合线的斜率，您就知道了方程 (5.4) 右侧的常数值。现在，您可以将左侧的值代入。将 $n_{\mathrm{atm}}$，即大气压下的空气折射率，作为未知值——这是您在排空气之前真空室的初始压力。
4. 对于左侧的其他三个值，您可以将大气压和真空中的压力（均以 cm Hg 为单位）以及真空的折射率代入。这将允许您计算空气中的折射率。
5. 将您计算的 $n_{\text {air }}$ 值与标准温度和大气压力下的已知来源（如 CRC 化学与物理手册）中的值进行比较。对结果进行评论。

8.3 一般问题

1. 迈克耳孙干涉仪可以用来测量极小的距离尺度。能够测量的最小距离尺度是多少？与之相关的误差是多少？如何提高精度？
2. 法布里-佩罗干涉仪能够测量的最小距离尺度是多少？哪一个更好，迈克耳孙干涉仪还是法布里-佩罗干涉仪？为什么？
3. 如何改变这些干涉仪中的任意一个，以测量更小的距离尺度？如果您希望使用本实验中的相同设备，该如何操作？

[^0]: ${ }^{1}$ 迈克耳孙的著名实验推翻了以太假说，促进了相对论的发展。 ”